From quantum chemistry to many-body theory of frustrated antiferromagnets
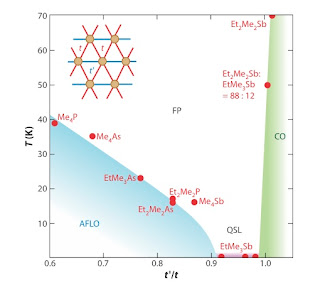
There are a wide range of organic charge transfer salts that can be described by a Hubbard model at half filling on the anisotropic triangular lattice. [See this review for a full discussion]. This model can also be viewed as a square lattice with hopping t' along one diagonal. An important parameter is the ratio t'/t. The values t'=0, t'=t, and t=0, correspond to the square lattice, isotropic triangular lattice, and decoupled chains, respectively. The actual value of t'/t is critical because the ground state of the Heisenberg model for the Mott insulating state [Neel, spiral order, valence bond crystal, spin liquid] is quite sensitive to the value of J'/J=(t'/t)^2. For example, as J'/J increases from 0.6 to 0.9 the order can change from Neel to valence bond crystal or spin liquid to spiral order. So, what value do specific materials have? Do they vary with the counter anion? Previously the parameters t and t' have been estimated from Huckel t







